Strength, stamina, and mobility have unique roles in aerial hoop including upper body strength, grip strength, and bilateral hip and leg flexibility and strength (Ruggieri & Costa, 2019). This page describes some facts and figures that give reference to the physical load placed on aerial artists.
The Theory
Aerial arts demand a greater capacity for upper body strength than other forms of artistic movement practices (Dongaz et al., 2024). The aerialist must coordinate strength and mobility to manipulate their bodies within the hoop. Notably, as the Tanya lifts her feet from the ground (Video 1.) she takes her full body weight into their hands and controls its movement up and down with their arms (Fig 1). Any deviation of center of mass on the horizontal plane (usually forward or backward) increases the force demand on the aerialist’s arms as they resist motion. We can suggest that the aerialist should reduce swinging on the horizontal plane in order to execute movements more efficiently.
- In order to ascend into the hoop an aerialist must use a point to hoist their body into the air, often using inversion techniques (Crow, 2021). Arms act as the stable force where the body rotates and shifts in relation to the shoulder joint (Video 1). Here, the fixed point (hands) resists the weight of the dancer and shoulder joint the fulcrum of rotation (Urbanczyk et al. 2020).
- Cossin et al. (2022) analysed the maximal forces exerted on a variety of aerial props and found 2.5-4.5 times body weight is exerted on an aerial hoop in three separate movements. This study demonstrates that dynamic body weight control and absorption of load is integral for aerial execution and performance.
- Ruggieri and Costa (2022) found in recreational aerial artists, grip strength was correlated to upper body strength. Aerials artists notably could perform a variety of pull ups and exhibited a significant strength difference between dominant and non dominant legs (Ruggieri & Costa, 2019, González Macías & Flores, 2024). It is likely to see some bilateral differences in aerial artists as many positions and movements function to split the legs in order to balance, working in the sagittal plane.
How to get better!
- Work to maintain similar strength and mobility capabilities bilaterally (Cossin, 2022)
- When inverting, don’t swing forward and back
- Direct energy up and down in order to resist body weight
- Train similar movement patterns to hoop moves
- Focus on shoulder joint strength and stability (Urbanczyk et al. 2020)
Quantifying load: Pike Entrance in 2 phases

The video and analysis show the control and load demanded during a pike inversion from when feet lift from the ground to the highest point of the hips. There is 573.44 N controlled by Tanya’s hand and arms. She keeps her center of mass (pelvis) very close to the center line and reduces force in the x axis.
Inversion to Pike (analysis)
Formulas:
△v = △d/t
a = △v/t
F = ma
Fapplied= √x²+y²
Inversion
Time: 2.57 sec
Mass: 58 kg
Position 1 (di) : 123.73, 98.13
Position 2 (d2) : 115.55, 148.88
Acceleration due to gravity: 9.81m/2^2
Distance x axis = 115.55 – 123.73 = -8.18 cm = -0.08 m
Distance y axis = 148.88 – 98.13 = 50.75 cm = 0.51 m
x axis
△v = 0.007m/s
a = 0.003 m/s^2
Fx = 0.16 N
y axis
△v = 0.20 m/s
a= 0.08 m/s^2
Fy = 4.46 N
Force gravity (weight)
Fg= 568.98 N
X component = 0.16 N
Y components = 4.46 N + 568.98 N = 573.44 N
Force applied = 573.44 N² + 0.16 N² = 573.44 N
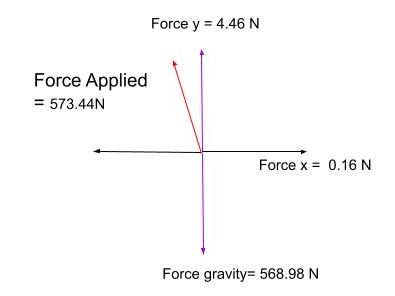
573.44 N exerted on arms and hands in the eccentric phase of a pull up in order to invert

In this rowing movement in order to lift herself into the hoop, Tanya pulls herself up and forward from the moment she grabs the hoop to seated. If she were to only rely on her arms, they may resist 573.02 N. Instead she is able to maintain a strong core and coordinate a slide into the hoop, and gradually offload her weight on the hoop.
Pull to Sit (analysis)
Pull to Sit
Time: 2.63 sec
Mass: 58 kg
Position 1 (di) : 79.91, 114.80
Position 2 (df) : 103.67, 163.02
Acceleration due to gravity: 9.81m/s²
Distance x axis = 103.67 – 79.91 = 23.76 cm
Distance y axis = 163.02 = 114.80 = 48.22 cm
x axis
△v = 0.09 m/s
a = 0.3 m/s²
Fx = 1.99 N
y axis
△v = 0.18 m/s
a= 0.07 m/s²
Fy = 4.04 N
Force gravity (weight)
Fg = 568.98 N
X component = 1.99 N
Y components = 4.04 N + 568.98 N = 573.02 N
F applied= √x²+y²
Force applied on arms and hands = √(573.02 N² + 1.99 N²) = 573.02 N
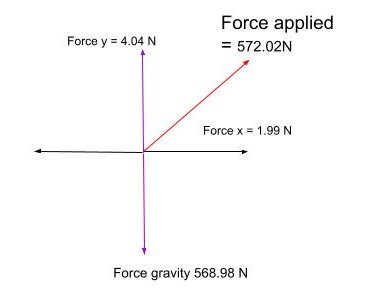
Force applied to lift and pull into the hoop = 573.02 N
*Note. This is the maximal force needed at the upper body in a rowing combined with a pull up action assuming weight is not relieved as the aerialist sits.
Limitations: due to the nature of the hoop rig, the camera and hoop could not be stabilized and calculations have a small margin for error.