Aerial arts have a remarkable rotational element. Aerialists move while suspended and spinning, often spinning so fast the audience can’t focus their eyes and aerialists appear as an evolving shape. With this, investigating the physical demand exerted on the body by an aerial hoop routine in relation to its unique use of physics spurs curiosity.
Spinning is one of the most exciting and unique elements of aerial arts. It can be very frustrating when the hoop slows or stops. Some may think to add more force to the spin when leaving the ground however the problem isn’t the speed of the spin at initiation, it’s the conservation throughout the routine. Gathered from the analysis below, as the Tanya’s limbs extend, the hoop slows, and as they retract, the hoop speeds up. The positions within the routine that change how far an aerialist’s body deviates from the center of the hoop control the momentum of the spin (Crow, 2021). If the aerialist wants to maintain the speed of the spin, or rotational velocity they need to ensure the routine includes a variety of positions that move limbs close and far from the area beneath the rigging point.
Quantifying the Spin
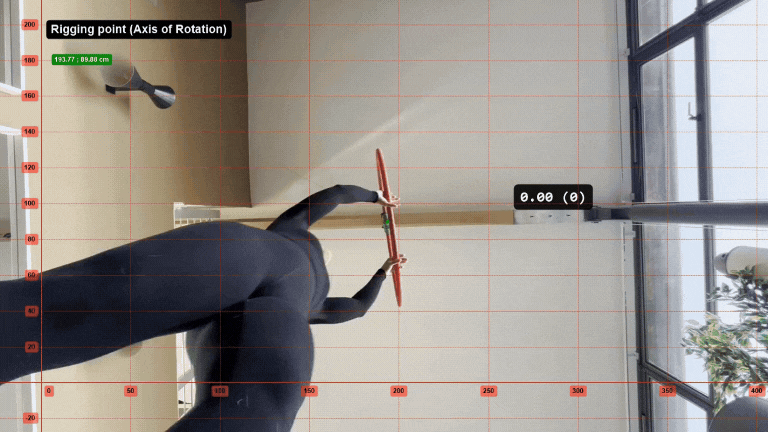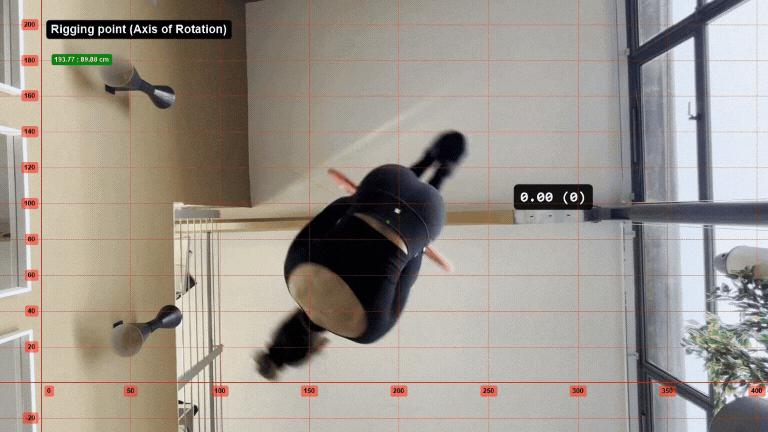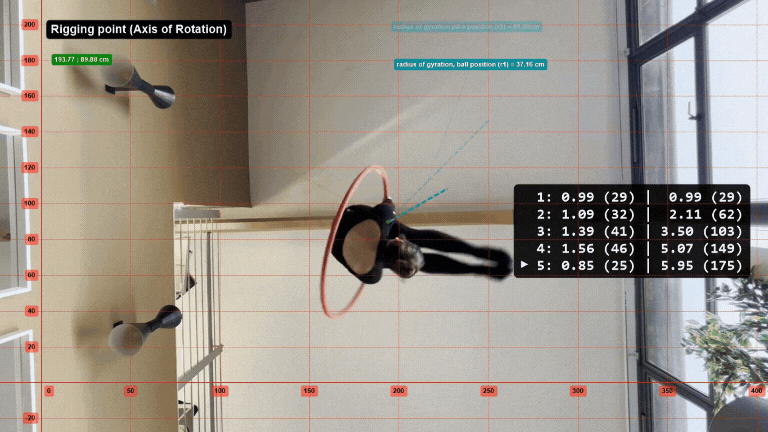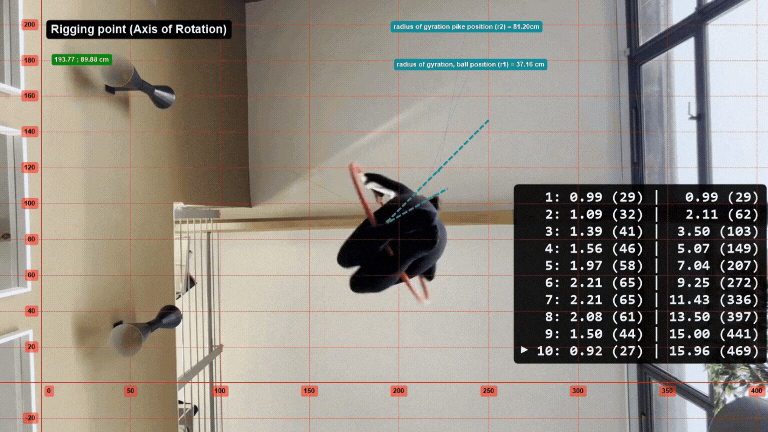
In the video above, as Tanya changes shape the rotation of the hoop slows. The calculations below determine how much she slows down in the pike position vs. tucked position.
The Math!
Formulas
Moment of Inertia (I) : I = m x r2
Angular Velocity : w = rad/s
Degrees to radians : rad =( deg)( 𝜋/180)
Acceleration: a = △ v /△t
Rotation 1. (tucked position)
Radius of gyration, r1 = 37.16 cm
1 revolution = 360 degrees
Time (t) = 0.99 sec
Mass Tanya = 58 kg
Mass hoop = 4.1 kg
Mass total (m) = 62.1 kg
w ave. = 6.35 rad/s
I = 8.58 𝑘𝑔⋅𝑚2
Rotation 6 (Pike position)
Radius of gyration, r2 = 81.20 cm
1 revolution = 360 degrees
Time (t) = 2.21 sec
Tanya mass = 58 kg
Hoop mass = 4.1 kg
Mass total (m) = 62.1 kg
w ave= 2.84 rad/s
I = 40.95 𝑘𝑔⋅𝑚2
Acceleration due to change in r
vi = 6.35 rad/s
vf = 2.84 rad/s
ti = 0
tf = 9.25 sec
a = -0.38 rad/s2
RESULTS: This change in position causes a negative acceleration of a = -0.38 rad/s2 by the end of the 3rd rotation in a pike.

The Theory
Angular momentum is the value assigned to the amount of movement an object has around an axis of rotation (Crow, 2021). The momentum can be increased or decreased due to a change in the radius from the axis of rotation of the object spinning. As the axis of rotation increases, the distribution of mass increases, this is defined as the moment of inertia (MOI)(Crow, 2021). The MOI influences velocity of the rotation; as seen in the video above. As the aerialist increases the distance of her legs away from the axis of rotation, the hoop slows. In this context the distribution of her mass is acting on the angular momentum, increasing the MOI and therefore decreasing the angular velocity of the hoop by 0.38 rad/s2. Eventually the hoop may slow to a stop. In order to conserve angular momentum and maintain the rotation of the hoop, reducing the radius of gyration can reduce MOI and there fore resistance against angular velocity (Crow et al.).
Aerialists can conserve angular momentum by organising choreography to vary the moment of inertia by adjusting the distance their body is from the rigging point. At the end of video 1. after extending her legs, the aerialist tucks them back into a ball and the hoop gains speed.
How to get better?
- Shapes that move limbs away and toward the inside of the hoop intermittently
- Maintain centre of mass under the rigging point
- Conserve momentum!